Dear All,
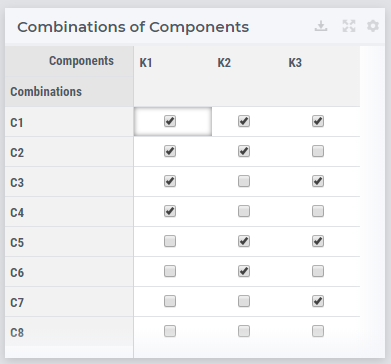
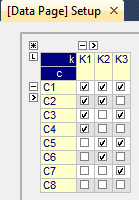
I want to generate an integer parameter based on the combination of a number of component as shown as:
| K1 | K2 | K3 | |
| C1 | 1 | 1 | 1 |
| C2 | 1 | 1 | 0 |
| C3 | 1 | 0 | 1 |
| C4 | 1 | 0 | 0 |
| C5 | 0 | 1 | 1 |
| C6 | 0 | 1 | 0 |
| C7 | 0 | 0 | 1 |
| C8 | 0 | 0 | 0 |
where K1 … Kn is the number of component and C1 .. Cn is generated combination based on component number. The value of 1 means that the component is available and the value of 0 is otherwise.
Is it possible to do this in AIMMS?
Thank you very much.
Best answer by Mischa
View original


 !
!