Hello,

Excuse the long explanation below. We are trying our best to make you understand the whole problem.

I am a Masters student currently conducting research on the University Examination Timetabling Problem (UETP) using Binary Integer Programming. The problem is the same examination problem whereby it is to assign exams to suitable slots and venues accordingly to the requirements stated (hard constraints). The number of exams to be assigned, the number of slots available, the number of rooms available are declared as SETS. Also, the same goes for the parameters such as the capacity of each room, students taking specific exams, specific courses that requires 2 hours or 3 hours of exams and etc are known in advanced. We have successfully formulated all the constraints into BIP. 

Just to let you know that we are executing all models through AIMMS.

Below are the constraints and objective functions involved in the model:

Constraints: (numbers of constraint below will be used in the table given)

(1) Completeness. All exams must be assigned to a venue at a timeslot.

(2) Conflict. No students can take more than one exam in the same venue at the same timeslot.

(3) Unavailable Timeslots. Certain timeslots are unavailable for exams.

(4) Room Capacity. The number of students assigned to each exam must not exceed the venue’s capacity.

(5) Gap. There must be a gap of at least two timeslots between exams taken by the same student (consecutive exams).

(6) Separation. 2-hour and 3-hour exams must be in separated room.

Objective Functions: (numbers of constraint below will be used in the table given)

(7) Preferences. This objective prioritizes scheduling exams according to specific student preferences. The preferences for assigning exam to venues at timeslots. These preferences are randomly given by AIMMS under the uniform distribution, where parameter value 5 is to the most preferred slot and venues and preference value of 1 if otherwise.

(8) Maximizing the number of exams assigned to the earliest timeslot possible. (2 weeks within the duration of the whole examination which is 3 weeks). This is detailed out in the table below.

(9) Maximizing the usage of the main venue DSM.

The objective function that can be illustrated for Objective Function t8].

Note: The coloured yellow boxes are the ones we defined as early slots (t = 1..30)

Thus, for these yellow boxes, we inserted the maximum preferences number (preference value of 5) if exams are assigned to these slots.

When running the model with all these constraints and objectives, the execution time becomes very long. After running the model for 5 to 9 days, the optimality gap was reduced to 0.38% and after 10 to 16 days, the gap only decreased to 0.37%, with the model still running. Here are the progress windows:

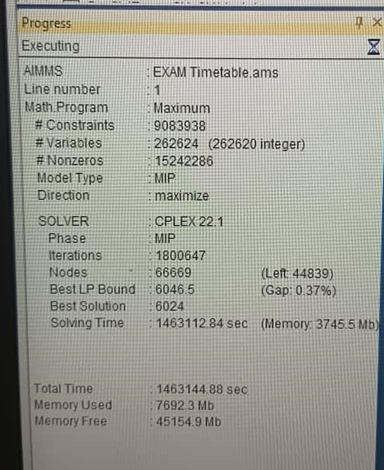
To give you a better sense of the performance, I ran the model on two different machines to compare results, both of which showed similar performance:

●        Server: Intel(R) Xeon(R) Silver 4214 CPU @ 2.20 GHz (2 processors), 16 GB RAM, Windows 10 Pro

●        Desktop PC: 13th Gen Intel(R) Core (TM) i7-13700 @ 2.10 GHz, 64 GB RAM, Windows 11 Pro

The 2 machines used are of the suggested specification by AIMMS experts (based on our previous conversation). Based on these two specifications used (as above), I believe that the memory capacity is sufficient to run the entire model, especially in terms of memory size, since he previously suggested using memory exceeding 50Gb.

Due to the large amount of data, I have also applied the following CPLEX options to optimize memory usage as suggested by him to my senior, Ms Zahidah. The suggestions listed below were given in that email. It worked on her mathematical model (obtained the Optimal Solution), the university course timetabling problem. Unfortunately, it did not work when solving my problem on a university examination timetabling problem that has a smaller data set (which confuses me more).

Suggestions given:

1. Aggregator : 0

2. Global thread limit : 1

3. Postsolve : Off

4. Infeasibility finder : On

5. Node file size : On disk and compressed

6. MIP method : Barrier

7. Solvers General option : All

8. CPLEX option ‘MIP display’ to ‘Nth node + info on node cuts’

9. CPLEX option ‘Parameter display’ to ‘Yes’

Just for your information, the email sent to Ms Zahidah:

To understand the problem better, I conducted several trials with different combinations of constraints and objective functions to observe each progress & hopefully to detect where the problem occurs. The trials were structured by complexity increment, starting from the simplest constraints to the hardest one.

We initially suspected that Constraint (4), (5) and (6) may be the ones contributing significantly to the prolonged execution time due to their complexity:

·Constraint (4): Room capacity. Ensuring that each exam’s assigned venue can accommodate the number of students.

·Constraint (5): Gap. Ensuring there’s a gap between consecutive exams for the same student.

·Constraint (6): Separation. Ensuring that 2-hour and 3-hour exams are scheduled in separate rooms.

Constraints (1), (2) and (3) are the basic constraints that did not cause any problem. Thus, our approach was to test Constraints (4), (5) and (6) one at a time with each objective function to determine whether these constraints or the objective functions might be contributing to the execution time problem.

Below are the results obtained:

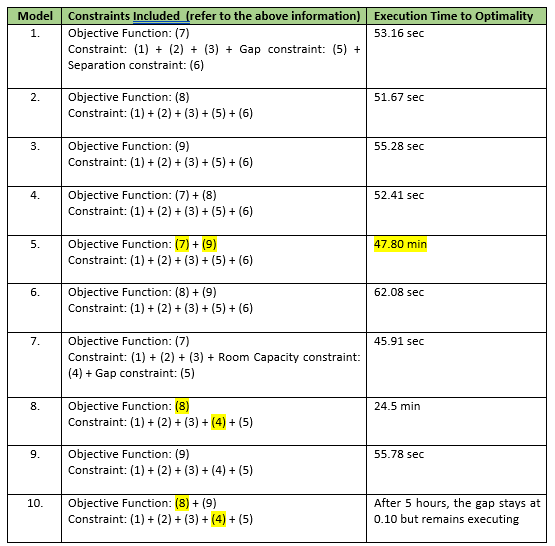
All combinations of constraints tested were able to reach optimality within a reasonable time frame individually, as shown in the table above. However, when combining Objective Function (8) and (9) with Constraints (1), (2), (3), (4), and (5) (refer to row 10), execution times significantly increased, with the model still running after 5 hours and the optimality gap remaining at 0.10 (as shown in progress window).

This prolonged execution time suggests that the slowdown may be related to the complexity introduced by combining Objective Function (8) and (9) with Constraints (4) and (5), as this combination seems to require significantly more processing time compared to simpler constraint sets.

Despite the seemingly reasonable execution times for individual constraints-objective functions, the full model, (1) + (2) + (3) + (4) + (5) + (6) + (7) + (8) + (9), still takes an excessively long time to run. I am unsure whether this is due to the complexity of combining all the constraints or another underlying issue.

This is what we can conclude:

(1)    For models 1 to 6, we believe the problems lies with objective functions (7) and (9), as objective function (7) involves random preference values, which may create variability due to the uniform distribution used in AIMMS. We highlighted Model 5, as it likely involves the random number in objective function (7), which could be contributing to longer execution times.

(2)    For models 7 to 9, we included constraint (4), and observed that Model 8 takes more execution time compared to Models 7 and 9. This could be due to the combination of constraint (4), (which stated that the number of students assigned to each exam must not exceed the venue’s capacity), with objective function (8), (which aims to minimize the number of exams assigned to the earliest timeslot possible. This combination may be causing the increased execution time.

(3)    We also tested different combinations of objective functions, and noticed that when constraint (4) is paired with objective function (8), execution time increases, as in Model 8 and Model 10.

Could you please advise on why this prolonged execution time might be happening, especially when running the full model, why is it taking such a long time to solve? Are there any strategies or solver settings in AIMMS that I could try to improve the performance of the full model? I believe that achieving an optimal solution should be possible, as we previously obtained optimal solution for a similar type of problem: University Course Timetabling Problem (UCTP) model in our earlier research, with a larger data set and more constraints considered but managed to achieve optimal solution.

If possible, could you please try running the full model on your machine specifications? This would help determine whether if the model correctly formulated or otherwise or if it needs other requirement adjustment. If you do agree, I could send the project to you.

Or, we could send u the specific problematic models (Model 5, Model 8, Model 10 and the full model with data) for u to test on your machine.

I would greatly appreciate your help on this matter as it is important for the progress of my research.Thank you in advance for your assistance.