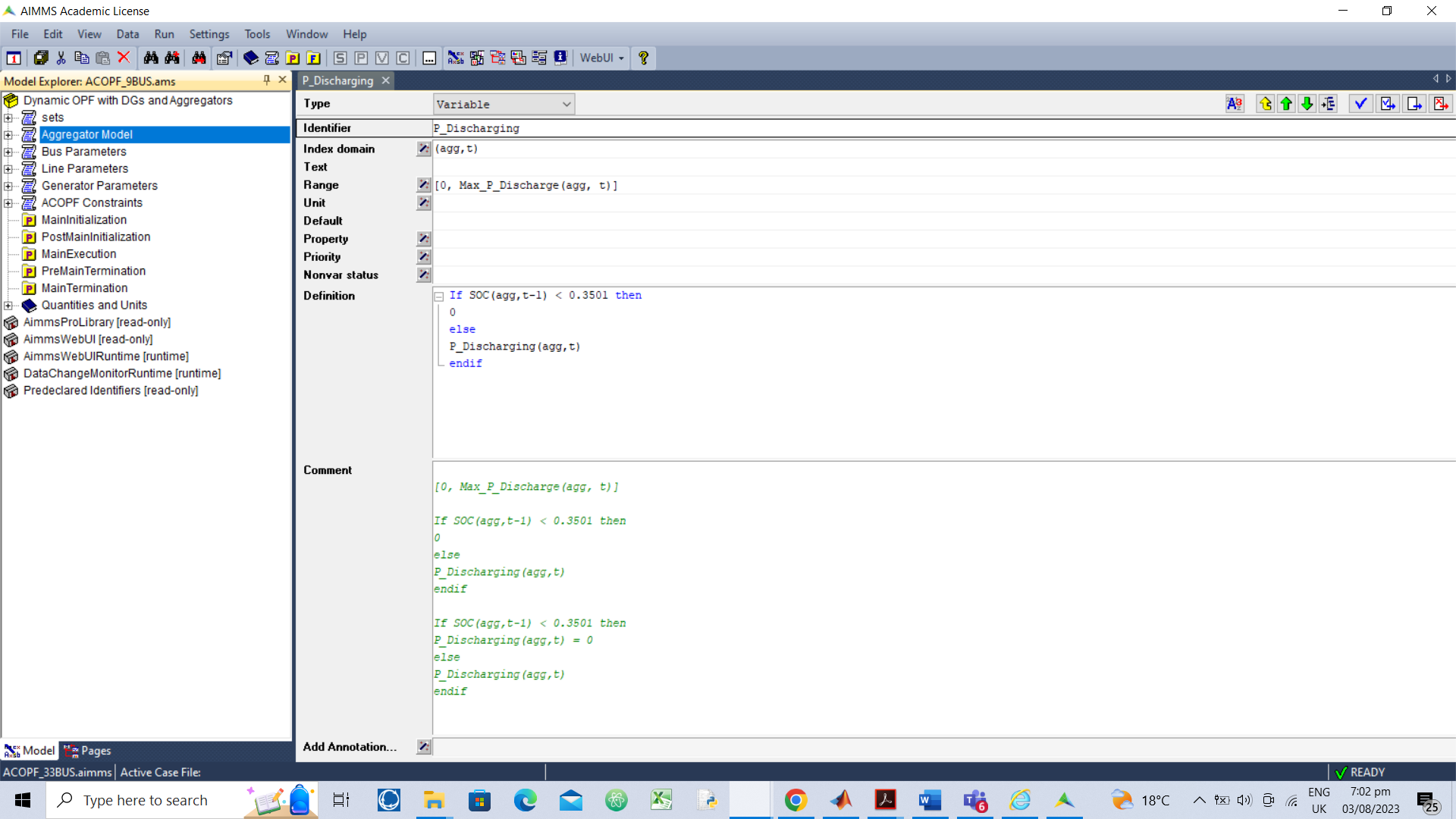
hi @olusegun.adeniji. Seems to me that you want to model for P_Discharging(agg,t): If SOC(agg,t-1) < 0.3501 then P_Discharging(agg,t) = 0.
Linear models cannot handle strict inequalities (<) so you have to use some kind of small (epsilon) value to transfer them into <=.
For P_Discharging(agg,t) you need a new binary variable, say X(agg,t). Then you need these new constaints:
SOC(agg,t-1) <= 0.3501 - eps + M*X(agg,t)
SOC(agg,t-1) >= 0.3501*X(agg,t)
Here M is some big value and eps a small (positive) value close to 0. Now you need one more constraint, namely
P_Discharging(agg,t) <= M*X(agg,t)
Now we have modelled:
- If X(agg,t) = 0 then SOC(agg,t-1) <= 0.3501 - eps, and P_Discharging(agg,t) = 0.
- If X(agg,t) = 1 then SOC(agg,t-1) >= 0.3501.
The current definition of P_Discharging should be removed.
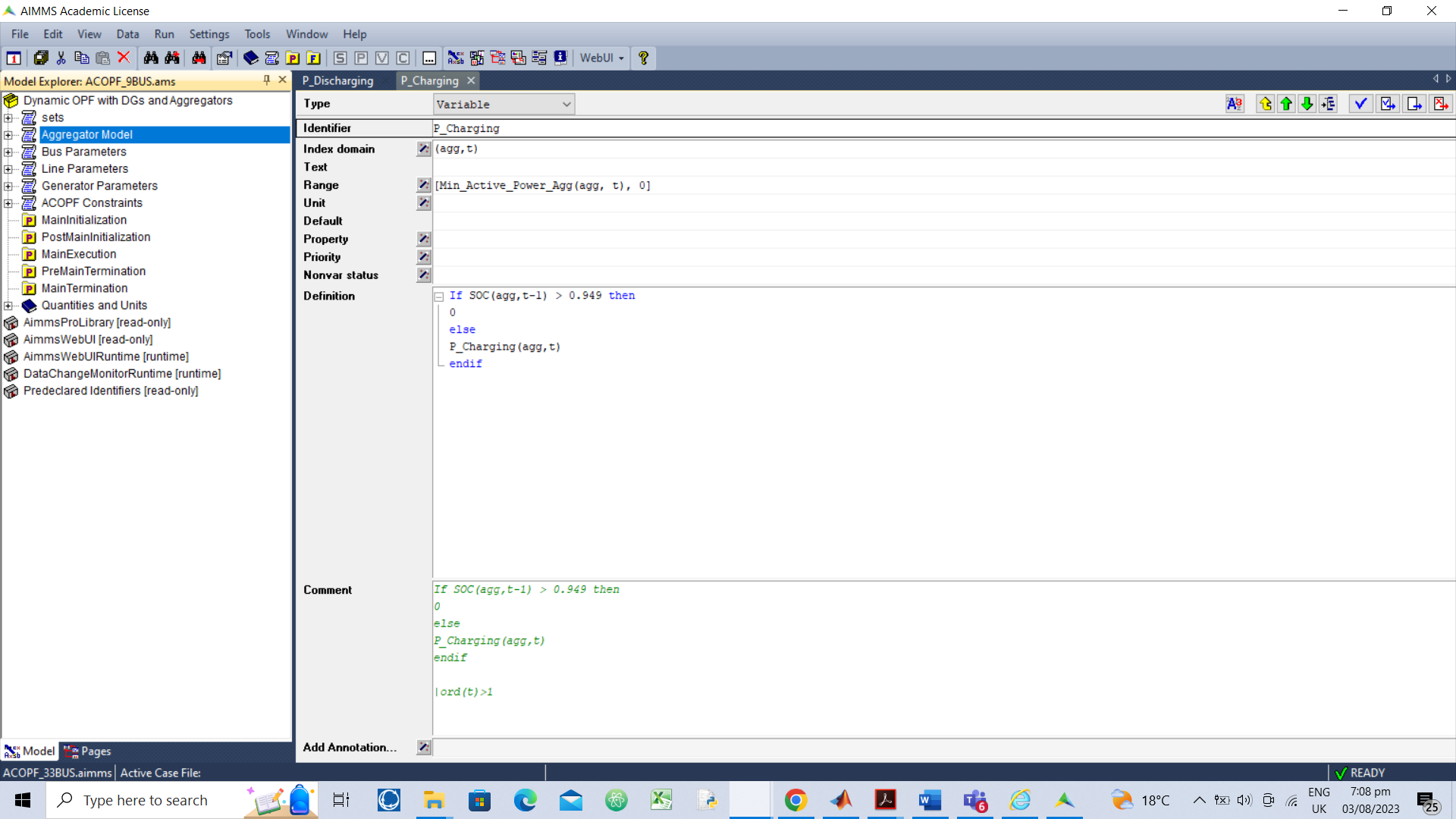
The variable P_Charging you can be reformulated in a similar way.
Thank you for your prompt response. I have implemented the P_Charging part as follows:
SOC(agg, t -1) >= 0.949 + eps + M*Y(agg, t);
SOC(agg, t - 1) <= 0.949 * Y(agg, t);
P_Charging(agg, t) >= M*Y(agg, t).
So if:
- Y(agg, t) = 0, then SOC(agg,t) >= 0.949 + eps, and P_Charging (agg,t) = 0
- Y(agg, t) = 1, then SOC(agg,t) <= 0.949.
But when I used a high value for M in the formulation, it returned that a high value cannot be implemented.
Olusegun
I think you should be using
P_Charging(agg, t) <= M*Y(agg, t).
(so different type). The M does not have to be very large. It suffices to make the M in the first constraint equal to an upper bound on SOC, so you can use Max_SOC(t). The M in the third constraint can be equal to Max_P_Discharge, because that defines an upper bound on P_Charging.
Hi,
By design, I modelled the P_Charging to be negative while P_Discharging is positive. So, the range of P_Charging is ((Min_Active_Power(agg, t), 0) while the range of P_Discharging is (0, Max_P_Discharge(agg,t)). The range of SOC(agg,t) is (Min_SOC(t), Max_SOC(t)). Both the ranges on SOC(agg, t) are positive.
So I think this will be finally right:
For Discharging:
SOC(agg,t -1) <= 0.3501 - eps + (Min_SOC(t) * X(agg,t))
SOC(agg,t -1) >= 0.3501 * X(agg,t)
P_Discharging(agg,t) <= Max_P_Discharge(agg,t) * X(agg,t)
For Charging:
SOC(agg, t -1) >= 0.949 + eps + Max_SOC(t) * Y(agg, t);
SOC(agg, t - 1) <= 0.949 * Y(agg, t);
P_Charging(agg, t) <= Min_Active_Power(agg,t) * Y(agg, t).
I would appreciate if you could make necessary comments on the above formulation.
Thanks