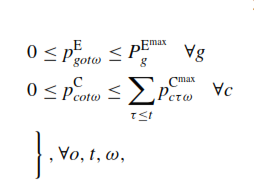Hello everyone
the following constraint
0<= P_cotw <= sum PMAX_c 'tau' w
'tau<=t
How can I declare the right side of the restriction
c, o, t, w subscripts.
'tau'
t = {1,2}
My case is:
Constraint LimProdCan {
IndexDomain: (c,o,t,s);
Definition: PotGenCan(c,o,t,s)<=CapConstruir(c,t,s);
}
Thank you
You will need to declare tau as a second index in the set T (same set to which t belongs). See this post for more details:
After declaring the second index, you can declare your constraint as
Constraint Constraint2 {
IndexDomain: (c,o,t,w);
Definition: P_C(c,o,t,w) <= sum)tau|tau<=t, P_CMax(c, tau, w)]
}
P_CMax’s original index domain is (c, t, w) but you replace t with tau (as it is another index in the same set) and limit the sum over tau to elements <= t.
tau <= t here will be equivalent to ord(tau) <= ord(t), assuming that your Set T is ordered i.e., t-1, t-2, t-3 … t-n
I am checking
Thank you
I got the solution.
Best regards
When solving the above problem, I am not getting the desired resolution.
Declare:
That belongs to the three Buses.
Set Buses {
Index: i, j;
}
{b1, b2, b2}
Then the parameters
Parameter Susceptance {
IndexDomain: (i, j);
}
Variable
Variable FlowLines {
IndexDomain: (i, j);
Range: free;
Definition: Susceptance (i, j) * (DeltaAng (i) -DeltaAng (j));
}
I don't know where the error is,
Since there is a power flow going from bus 1 to bus 2
bus 2 to bus 3, bus 1 to bus 3 and vice versa.
How can I declare what is blue in the constraints (Image above).
j belongs to set i
If you can support me, thanks.
You might want to update your variable declaration as below for efficiency.
Variable FlowLines {
IndexDomain: (i, j)|i <> j;
Range: free;
Definition: Susceptance (i, j) * (DeltaAng (i) -DeltaAng (j));
}
Now, the constraint highlighted in blue can be declared as
Constraint1 {
Index domain: i
sum
}
Now, you say j belongs to set i but the image shows j belongs to omega(i). What does omega(i) represent ?
In summary
The problem has three nodes or buses, unit 1 is on bus 1 and unit 2 is on bus 2. Demand (triangle) on bus 3.
finally there are three lines or links.
Line 12 means that it is connected from bus 1 to bus 2.
Line 13 means that it is connected from bus 1 to bus 3.
Line 23 means that it is connected from bus 2 to bus 3.
is where the problem is.
Now if I am on bus 1 there are two power flows that go through the lines, the flow that goes from bus 1 to bus 2, from bus 1 to bus 3. The same thing happens if I am on bus 2 now it is the flow that goes from 2 to 1 and from 2 to 3. mathematically it is the suscepatancia by the difference of angles.
so that would be the Omega set
Ωi where i = 1,2,3 are the buses
Ω1 = {2,3}
Ω2 = {1,3}
Ω3 = {1,2}
then I have
the generation units set
the Demand set.
the set Nodes or buses (which has two indexes i, j)
the developed model would look like this:
my other idea is to declare the set Lines as:
{Line1, Line2, Line3} or {1,2,3} or {Line12, Line13, Line23}
but as I tell AIMMS that Line1 goes from node 1 to node 2.
Line2 goes from node 1 to node 3 and line3 goes from node 2 to node three.
It should be noted that the power flow goes in both directions
1 to 2, 1 to 3, 2 to 1, 2 to 3, 3 to 1 and 3 to 2 therefore the 3x3 matrix(3 buses) and the i and j indices.
Finally, as I declare that generator 1 is on bus 1, generator 2 is on bus 2 and the demand is on bus 3.
Already have an account? Login
Please use your business or academic e-mail address to register
No account yet? Create an account
Enter your E-mail address. We'll send you an e-mail with instructions to reset your password.
Didn't find what you were looking for? Try searching on our documentation pages: